Our next discussion covered how to determine the optimal roundness of a particular shape or object's image. We described optimal roundness as the minimization of the ratio between the radius of the circumscribed and inscribed circles of a polygon. We then aimed to measure how round a convex polygon's image could be made using particular types of transformations.

Version 1: Affine Transformations

Our first attempt dealt with solely affine transformations, specifically rotating or scaling along an axis. Testing randomly generated convex polygons, we created a program which repeated this affine optimization procedure until no further iterations improved the image’s roundness:

1. Locate the longest axis of the image
2. Rotate the image such that the longest axis was parallel to the x axis
3. Scale the image down by some fixed constant along its longest axis
4. Rotate the image back to its original orientation

Version 2: Affine and Projective Transformations with Bug

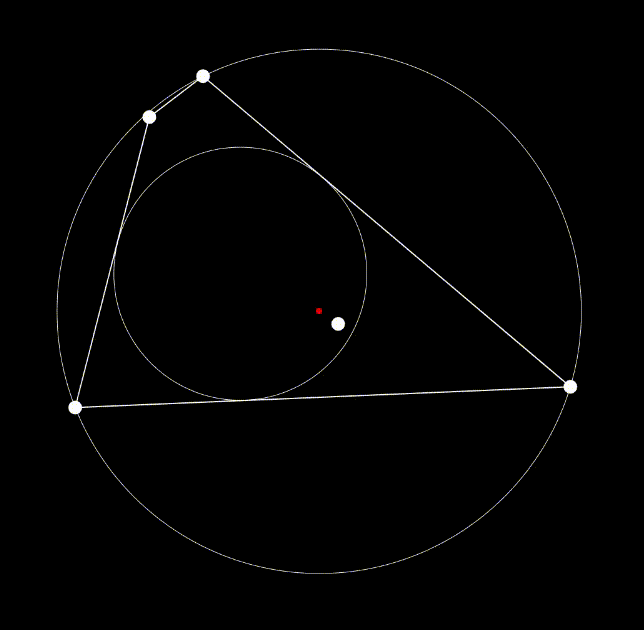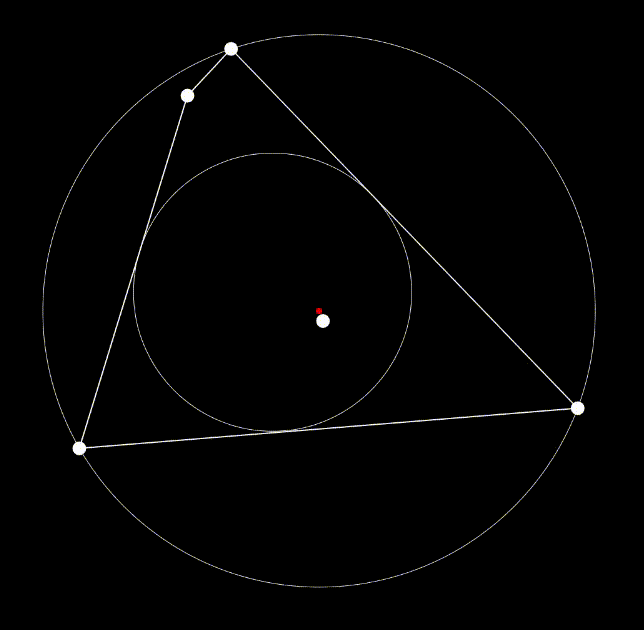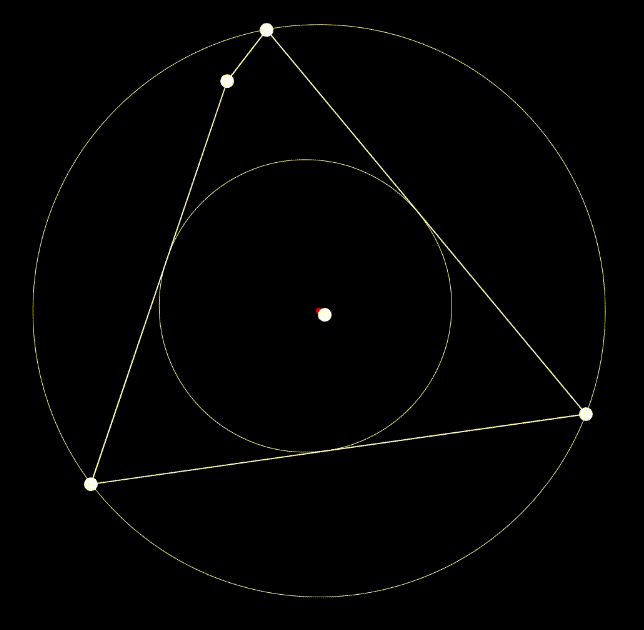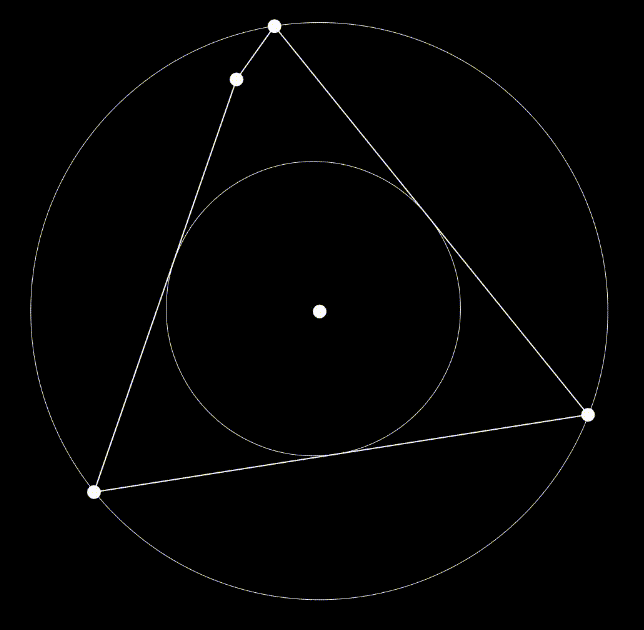
The second version of the program combined affine and projective transformations in sequence, with a pair of affine and then projective transformations constituting a single step in the iterative process. The projective optimization was nearly identical to the affine optimization, except with a projective transformation (incrementing elements i or j in the projective linear transform matrix) replacing step 3 in the procedure listed above. For visual aid, we displayed the axes of optimization using lines colored red (for affine transformations) and blue (for projective transforms between the bug and the “center” of the polygon).

We also combined roundness optimization with a similar concept of the “bug” from the  previous experiment; we determined how to increase the roundness of the projection in such a way that the image of a “bug” placed on its surface appeared to move towards the center of the projection. The center of the projection could be defined as any arbitrary point within the polygon, and the experiment still functions as intended (we experimented with the polygon’s center of mass, the inscribed circle’s center, and the average between the circumcircle’s center and the inscribed circle’s center). We selected the polygon’s “center” to be the center of its circumcircle; we found that this definition resulted in more direct movement of the bug toward the center. In this context, the “longest axis” referred to by the optimization procedure is locked in as the distance between the center and the bug.

Testing this program with convex polygons of up to one hundred vertices, we can observe consistent results regarding the image’s lower bound of roundness. With the added constraint of the bug, the minimum roundness is about 0.5 (comparative to that of an equilateral triangle, seen in figure A). Without the bug, the minimum roundness is about 0.7 (comparative to that of a trapezoid, seen in figure B). These convergences are a result of successive projective transforms which appear to “squish” all but two or three vertices into one vertex, so that the final image appears to have only three or four vertices (depending on if the bug is present or not). Polygons with greater number of vertices tend to generate with higher roundness, as they are convex. In these cases, if the bug is present, one can move the bug far from the center to observe how the projective transformations compress vertices on the opposite side together.

Below: typical performance of final version of algorithm; note that projective transforms are generally used less often than affine transformations