At the end of last semester, we had an idea for a new searching algorithm that we called 'image patching'. You can read more about our initial idea on the old project page here.
New Visualization Tool
Our previous algorithms were able to find some valid intervals for smaller groups, but as after moving to the (3,4,4)-triangle group, our visualization of \(\mathbb{RP}^1\) as a circle started to become crowded and difficult to debug (it is known that the valid intervals for this group needed to cover all of \(\mathbb{RP}^1\)). To solve this visualization problem before continuning to work on the algorithm, we decided to display each disconnected interval on its own copy of \(\mathbb{RP}^1\) which we represented as horizontal lines which wrapped around. This gave us the much more satisfying image below:
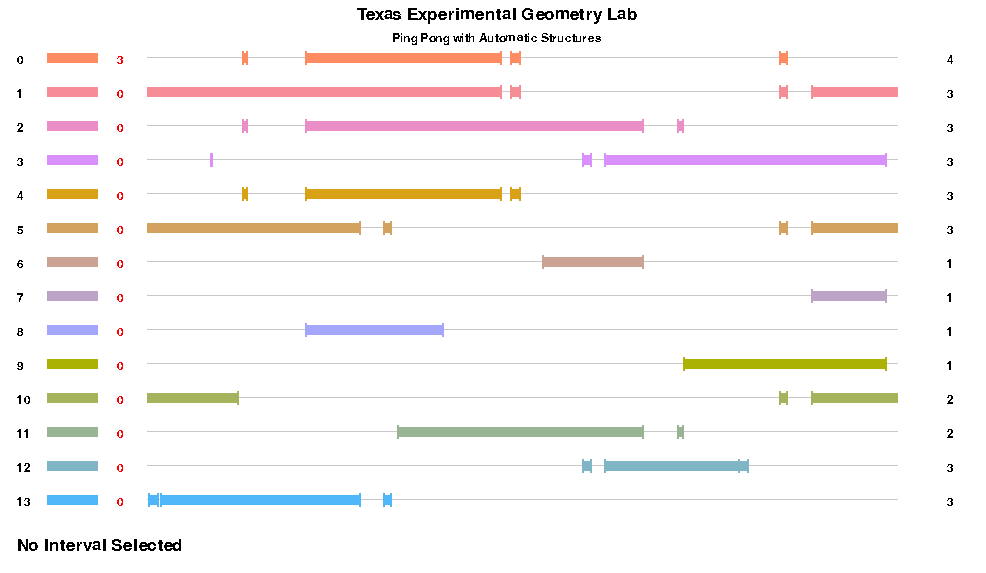
Intializing Intervals
As before, we initialize intervals around the singular directions of words of reasonable length (usually 5-7 letters) which are selected by taking paths along the automatic structure which represents the particular group presentation we are using. The idea of this was that since valid intervals must contain the singular directions of infinite length words of the graph, we can approximate these spots with shorter words to start our search. For each of these singular directions, we initialize a small interval around it with interval endpoints plus or minus \(\epsilon\) from the angle of the singular direction.
Patching Intervals
Our previous algorithms all tried to then expand these intial intervals, checking if they were valid at each step. They usually each had the flaw of expanding too far, skipping over what would have been valid intervals. This was where we had the idea for image patching. Each interval would expand by exactly the amount that it needed to at each iteration. This would mean that we would never expand more than necessary guaranteeing we would find valid intervals if they did in fact exist (assuming the initial intervals were placed in a reasonable enough location).
Algorithm Pseudocode
The algorithm can be broken down as follows:
A) For each node of the graph associated to the group presentation, do the following:
1) Initialize an empty disconnected interval for the current node.
2) Recursively find all words of length 5 starting from the current node (paths of length along the graph)
3) For each word, do the following:
i) Find the matrix representation of the word by multiplying all of the \(SL(2,\mathbb{R})\) representations of the letters together from right to left.
ii) Get the SVD of the matrix representation and find the location of the singular direction associated with the largest singular value in \(\mathbb{RP}^1\).
iii) Initialize an interval with endpoints plus or minus \(\epsilon\) from the singular direction and add it to the disconnected interval for the current node.
B) Patch intervals according to the following until valid intervals are found:
1) For each disconnected interval:
i) Initialize an empty list of failed containments
ii) For each disconnected interval which must be contained in the current interval according to the graph associated to the group presentation:
a) Find the image of the disconnected interval under the letter associated with edge connecting the two disconnected interval's nodes.
b) If the images of any of the components are not contained in the current disconnected interval, add them to the list of failed containments.
iii) For each failure, create a new interval with endpoints plus or minus \(\epsilon\) of the failed interval and add it to the current disconnected interval.
iv) Merge all of the intervals in the current disconnected interval.
2) Check if any of the disconnected intervals cover are equal to \(\mathbb{RP}^1\). If any of them are, the search has failed.
3) Check all of the containments of the new disconnected intervals. If none of them have failed containments, we have found valid intervals.
This summarizes the general idea of the algorithm. There are many small optimizations we use that are not included in this description but following exactly what is outlined here will still define an algorithm which works to find the desired intervals.
See the code on GitHub here: https://github.com/CapSnCrunch/TXGL
