Given a set of two-dimensional tiles, the nature of the planar tilings that they admit arises from a deep interaction between the local and the global.  Aperiodic sets of tiles walk a fine line between order and disorder, admitting tilings, but only those without any translational symmetry, never permitting the simple repetition of periodic tiling. Their study dates to Wang’s work on the then remaining open cases of Hilbert’s Entscheidungsproblem. Wang encoded fragments of what are now known as Wang tiles, congruent squares with coloured edges, to be tiled by translation only with colours matching on adjoining edges. He conjectured that every set of Wang tiles that admits a tiling (possibly using only a subset of the tiles) must also admit a periodic tiling, and showed that this would imply the decidability of the tiling problem (or domino problem): the question of whether a given set of Wang tiles admits any tilings at all. Berger then showed that it was undecidable whether a set of Wang tiles admits a tiling of the plane. He constructed the first aperiodic set of 20426 in 1964.

Perhaps in part due to the underlying undecidability of the tiling problem, there remain remarkably few truly distinct methods of proving aperiodicity in the plane.

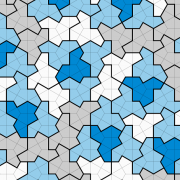
A longstanding open problem asks for an aperiodic monotile, also known as an “einstein”: a shape that admits tilings of the plane, but never periodic tilings. We answer this
problem for topological disk tiles by exhibiting a continuum of combinatorially equivalent aperiodic polygons. We first show that a representative example, the “hat” polykite, can form
clusters called “metatiles”, for which substitution rules can be defined. Because the metatiles admit tilings of the plane, so too does the hat. We then prove that generic members of our
continuum of polygons are aperiodic, through a new kind of geometric incommensurability argument. Separately, we give a combinatorial, computer-assisted proof that the hat must
form hierarchical—and hence aperiodic—tilings.
[Excerpt from https://arxiv.org/pdf/2303.10798.pdf]

Read more: https://www.quantamagazine.org/hobbyist-finds-maths-elusive-einstein-til...