Once the point group of a molecule is known, we can begin to make use of character tables. Group theoretical considerations and matrix algebra have produced a solid mathematical foundation for the information found in character tables. However, it would be too lengthy and beyond the scope of this course to cover this material rigorously. Fortunately, it is not necessary to have a full and complete understanding of the background theory in order to be able to use character tables to solve problems related to symmetry. We will approach the material from a more descriptive view point.
What is a Character Table?
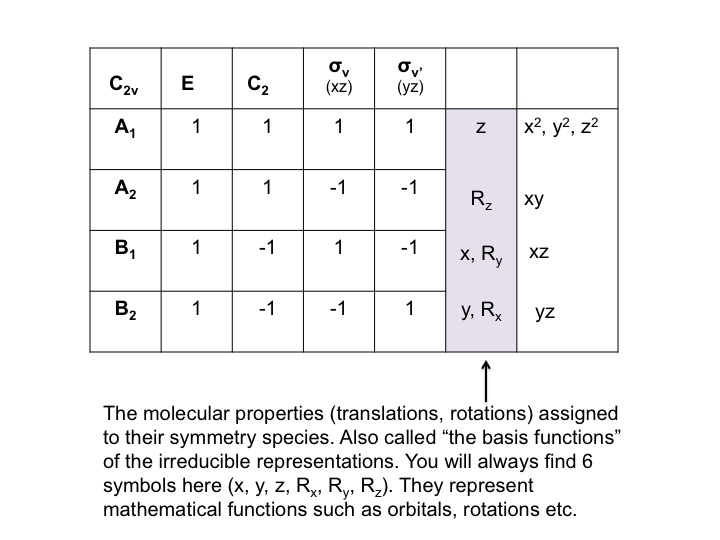
As we shall shortly discover, each point group has its own unique character table which is a device containing useful symmetry related information. A simple way of thinking about how a character table is constructed is to firstly, recognize that the positions of the atoms of a molecule (let's say water for example) conform exactly and precisely to the symmetry operations for the point group to which it belongs (C2v for example). That is, the appearances of the molecule before and after a symmetry operation are identical. However, molecules have other important properties which do not behave in exactly the same way as the positions of the atoms. These properties are often referred to as molecular properties, and can include simple translations, rotations, vibrations, and even the behavior of electrons in atomic orbitals. They are also referred to as "basis vectors."
An example of how we might generate information relating to a particular molecular property is to first agree to characterize symmetric behavior at +1 and antisymmetric behavior as -1, and to call the +1's and -1's the character of the property with respect to the symmetry operation. For water, we place the O atom at the origin of the cartesian coordinate system and examine the behavior of the Px orbital on O. [Note that the + and - in the figure refer to the angular dependence of the wave function.]
We now perform one of the symmetry operations for C2v (ignore the positions of the O and H atoms for the moment). If we choose the C2 operation then we would rotate the molecule about the Z axis.
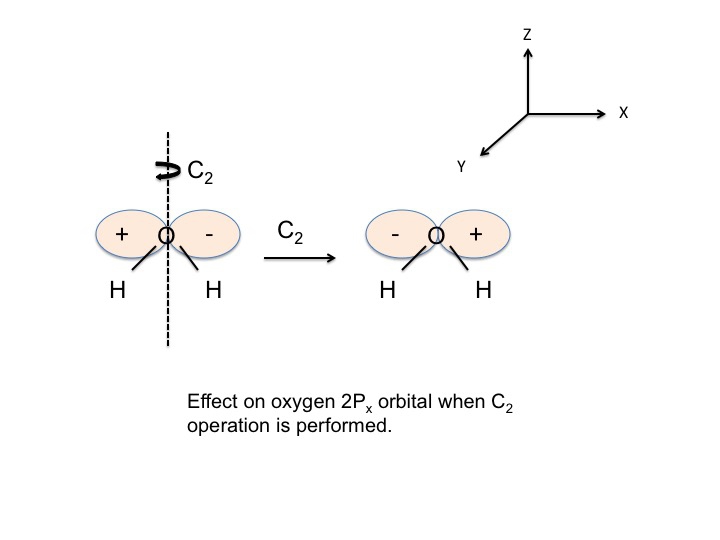
The sign of the wave function changes and we describe this as antisymmetric behavior and give it the character -1. We can perform this analysis for all four operations for C2v and tabulate the results.

A similar treatment for the oxygen Py and Pz orbitals gives the following table
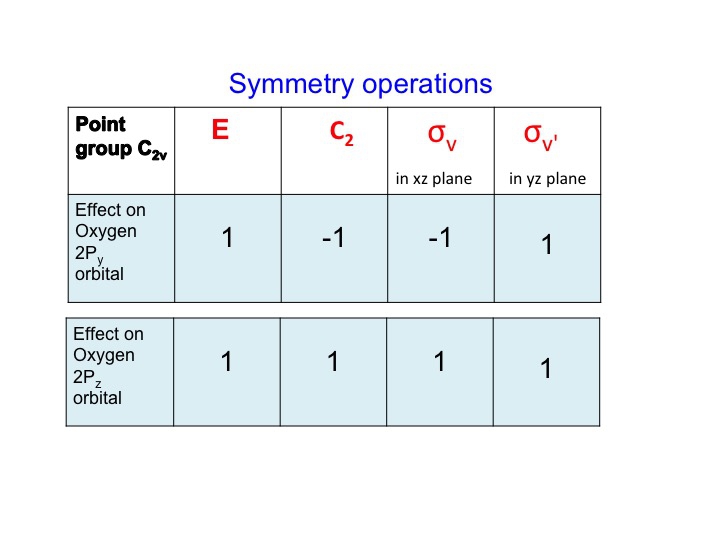
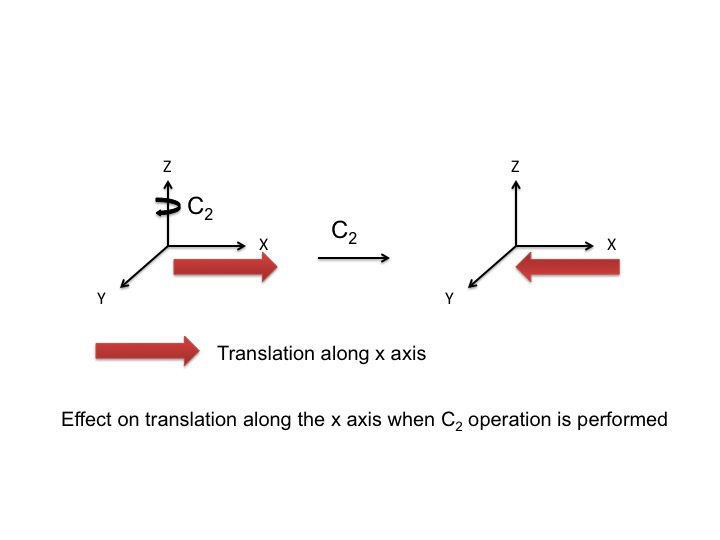
At this point we should also point out that the P orbitals lie along the x, y, and z axes, and the information that we have generated in the tables can equally be used to describe translations of the molecule. A translation is the movement of a molecule as a whole. Tx stands for translation along the x axis, and this can be depicted as an arrow pointing along the x direction. Performing the C2 operation reverses the direction of the arrow and so we assign this a -1 character (just like a Px orbital). Since we live in a 3-dimensional universe, there are three translations Tx, Ty, and Tz representing three degrees of freedom for the molecule.
In much the same way as we treated P orbitals and translations (by "inspection") we can also consider rotations of the molecule as a whole. Again, there are three possible rotations Rx, Ry, and Rz which can be performed by rotations about the x, y, and z axes respectively. Consider the rotation Ry as if it were the steering wheel of an automobile - depicted here with a curly arrow. After the C2 operation, the direction of turn of the automobile has been reversed (clockwise to anticlockwise) and so we assign a -1 character.
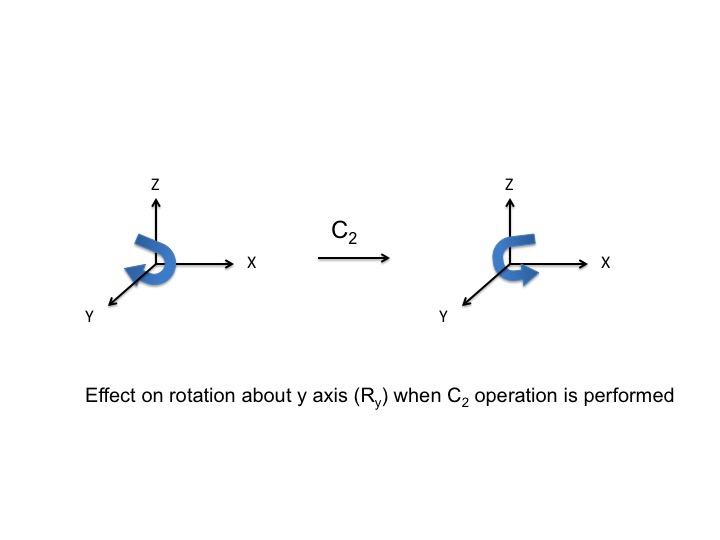
For Ry, a table of the effect on rotation about the y axis looks like this (rotations about the x and y axis have also been added)
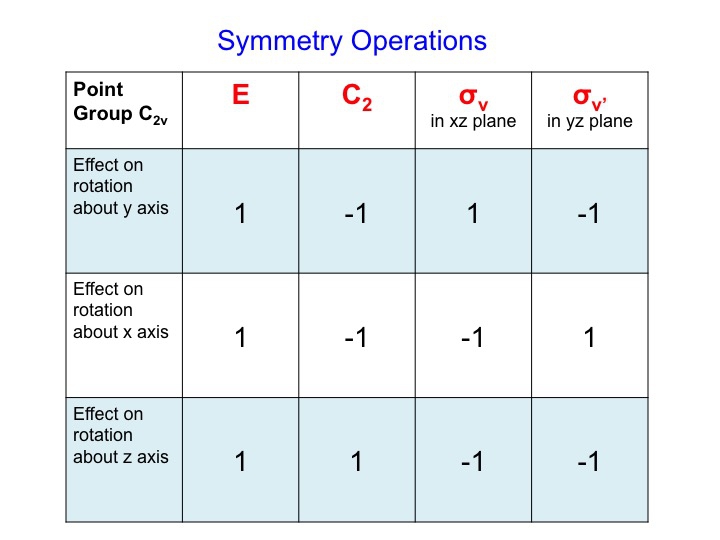
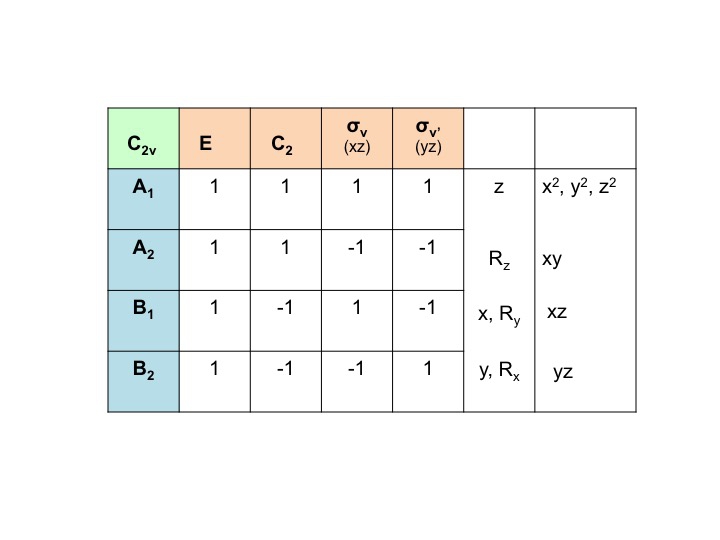
We can condense this information about the molecular properties of water into a table - a Character Table. The character table for water (C2v) is shown below

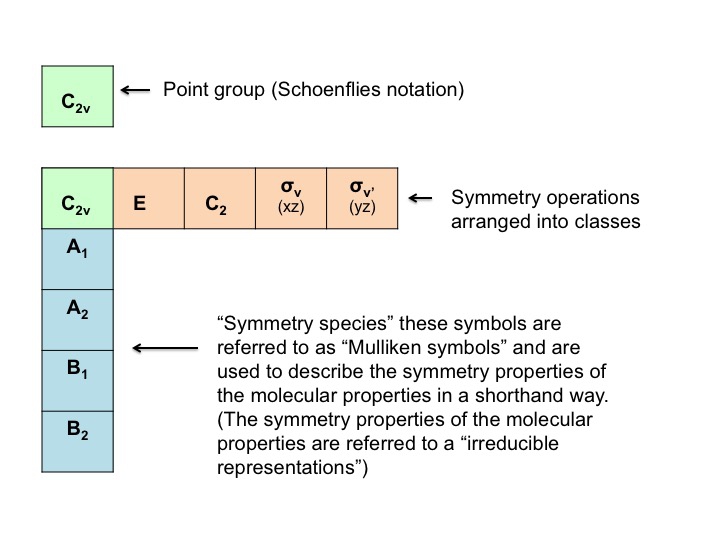
The various parts of the table can be described as follows [Note that some of this nomenclature comes from the mathematical underpinning of group theory - don't be put off by it!]

 What do Mulliken Symbols Stand For?
What do Mulliken Symbols Stand For?
 Robert S. Mulliken
Robert S. Mulliken
Mulliken symbols were proposed by Robert S. Mulliken (1896-1986, Nobel prize in chemistry 1966) and are intended to have the following meanings:
A or B stand for one dimensional representations
A - is symmetric with respect to rotation about a principal axis (Cn)
B- is antisymmetric with respect to rotation about a principal axis (Cn)
E - stands for a doubly degenerate representation
T - stands for a three dimensional representation
Subscripts 1 and 2 refer to symmetry with respect to a C2 axis perpendicular to a principle axis (Cn), or to a vertical plane of symmetry if there is no C2
1- symmetric
2 - antisymmetric
Primes (') or ('') stand for symmetric (') or antisymmetric ('') with respect to a horizontal plane of symmetry (σh)
In point groups which have a center of symmetry (i) the subscripts g and u stand for
g - symmetric
u - antisymmetric
with respect to inversion.
A Few Last Comments about Character Tables
In this course you will NOT have to:
1. Determine the characters of an irreducible representation
2. Generate or create a character table or memorize any
3. Perform complex math using character tables
You WILL have to be able to use character tables and you will always have access to them if you need to use them for an exercise.
This website will serve as a useful resource to look up any character table.
Next: Normal Modes of Vibration
Copyright © 2015 Richard Jones. All Rights Reserved.

