Proper Rotations - Rotation by 360o/n
This is simply rotation about an axis, which passes through the molecule by an angle of 360o/n (or 2π/n). When repeated n times, the molecule returns to the original orientation. The appearance of the molecule must be exactly the same after the operation.
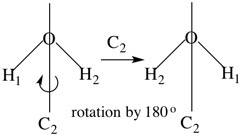
Example 1. H2O
H2O has a C2 axis - rotation by 360o/2 (180o). The axis passes through O and bisects the line between the H atoms. This operation interchanges the H atoms as well as the O-H bonds. Since these atoms and bonds are equivalent, there is no detectable difference after the operation.
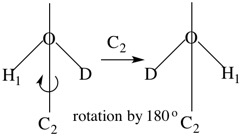
For HOD the C2 operation results in the molecule having a different orientation. Therefore, for HOD, C2 is NOT a valid symmetry operation.
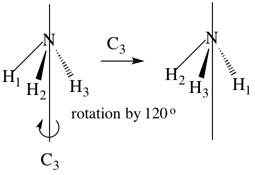
Example 2. Ammonia, NH3
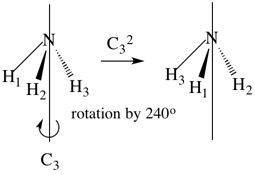
This molecule has a 3-fold rotation axis (a C3 axis) where rotation by 360o/3 (120o) produces an indistinguishable molecule (C3). Rotation by 2 x 120o also produces a configuration which is physically indistinguishable from the original (C32). Finally, rotation by 3 x 120o (360o) returns the molecule to its initial position (C33). This is equivalent to performing no operation at all, and we can say that C33 = E where E is the identity operation. We include E for mathematical reasons. There are therefore two symmetry operations associated with the C3 axis (C3 and C32).
When only a single rotation axis is present, it is assigned to the Z axis by convention. If more than one rotation axis exists, the Cn of highest order (highest value of n) is assigned as the Z axis.
Note - the proper rotation operation (Cn) is the ONLY operation we can actually perform on either a real molecule or its macroscopic model. The remaining operations (σ, i, Sn) are non-feasible and we have to use our imaginations a little to see how they work - they have to be visualized.
Next: Reflections
Copyright © 2015 Richard Jones. All Rights Reserved.

