What use are character tables?

At this point a good question is: what's the point of learning about character tables? The simple answer is that the symmetry and associated character table of a molecule can be used to interpret and predict many aspects of chemically significant spectroscopies as well as bonding. We will illustrate this next by focussing on the vibrational modes of a molecule.

In the laboratory we can gather useful experimental data using infra-red (IR) and Raman spectroscopy. This data can be compared to the number of IR and/or Raman active bands predicted from the application of group theory and the correct character table. The mathematics (group theory and matrix algebra) behind this treatment serves as a solid theoretical foundation. The manipulations described below work because all the symmetry operations of a molecule comprise a mathematical group and obey the rules of the group. As noted previously we do not have to master this area of mathematics in order to make good use of character tables.

Degrees of Freedom and Vibrations in Molecules

Here we will initially discuss the degrees of freedom for a simple molecule (water). We will very quickly see why it is very beneficial to employ symmetry when investigating larger molecules.

For a molecule with "N" atoms there are 3N degrees of freedom (remember we live in a 3-dimensional world of x, y, z coordinates). For a non-linear molecule 3 degrees of freedom can be signed to translations - movement of a body as a whole (T_x, T_y, T_z) and 3 to rotations (R_x, R_y, R_z). The remaining motions of the atoms are displacements of the atoms from their mean positions - the center of gravity does not change. These fundamental vibrations are referred to as "normal modes". Thus, a non-linear molecule has 3N-6 normal modes. For water the number of normal modes is 3 (3 x 3 - 6 = 3). For linear molecules there are 3N-5 normal modes.

For water, which of course has been intensively studied we know that the 3 vibrations are as follows.

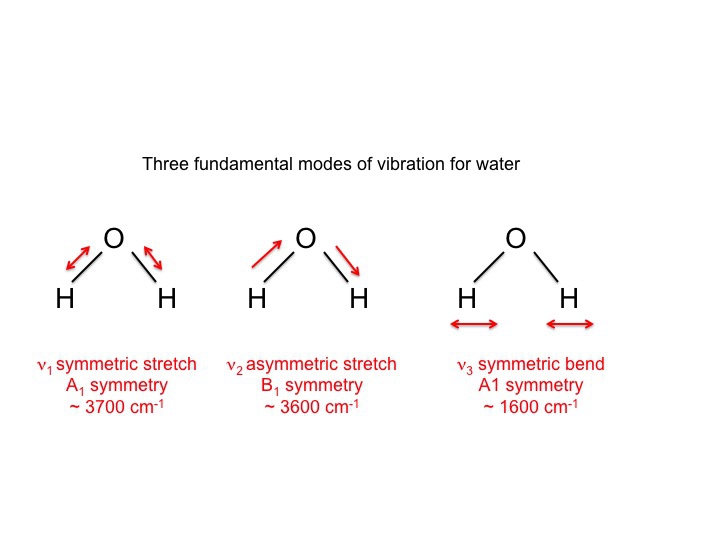
The symbols used to describe these modes (A₁, B₁) are the same Mulliken symbols that we encountered in our discussion of character tables. In other words, the vibrations, which are molecular properties, can described by symmetry species or irreducible representations. In fact much of the literature involving vibrational spectroscopy uses these symbols as a shorthand way of communicating information.

It should be pretty obvious that the number of vibrations increases rapidly with even modest increases in the number of atoms in the molecule. Determining the kinds of vibrations by inspection (as we did for water) now becomes much more difficult. For example consider the following compounds:

H₂O           3 atoms      3 vibrations

PH₃           4 atoms      6 vibrations

CO₂^2-        4 atoms     6 vibrations

XeF₄          5 atoms     9 vibrations

B₂H₆          8 atoms    18 vibrations

For diborane (B₂H₆) which has D_2h symmetry figuring out the nature and symmetry species of all 18 vibrations by inspection would be a daunting task. However, armed with the character table for D_2h and knowledge of symmetry properties the task of determining the symmetry species of all vibrations is straight-forward.

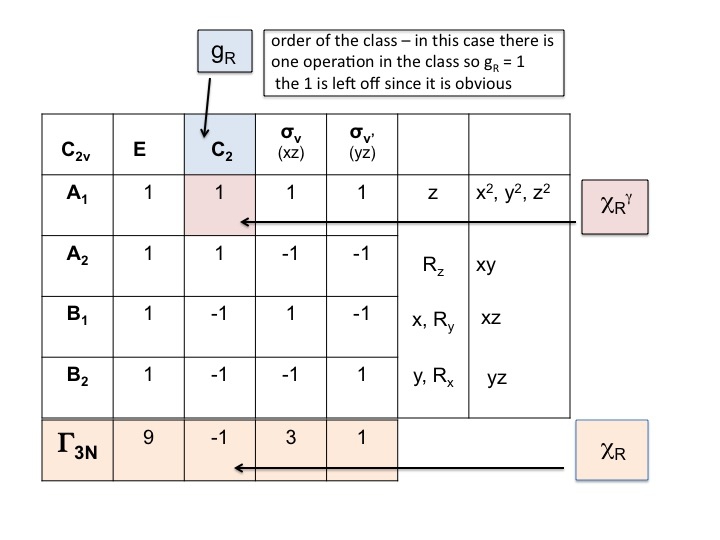
For the case of water we could present the character table (C_2v) with the 3 vibrations (ν1, v2, v3)  listed in the column of molecular properties as shown below. (ν = Greek symbol "nu")

However, in general this approach is impractical. Take pyridine (C₅H₅N) for example. The point group is also C_2v but the molecule has 11 atoms. The number of fundamental modes of vibration is 27 ( 3 x 11 - 6 = 27).

In this case we would have to draw up a C_2v character table showing the symmetries of all 27 vibrations. For this reason vibrations are not normally included in character tables. Instead it is up to the user (you) to determine the number and type of vibrations (as defined by their symmetry species) for any molecules that are encountered. How we do this is described below. 

Reducible Representations

As previously noted one of the important properties of character tables is that the symmetry operations are members of a mathematical group and important relationships exist between them. In general the same can be said about the symmetry species or irreducible representations of the molecular properties. The products from combining the characters of irreducible representations either by multiplication or addition/subtraction also obey the rules of the group. The new representations are no longer the most simple possible and are referred to as "reducible representations" because  they can be "reduced" down to their component parts.

For example, for water the symmetries of the translations (T_x, T_y, T_z) can be gleaned directly from the C_2v character table. They are A₁, B₁, and B₂. We can represent all three of these degrees of freedom by a representation Γ_T and we can write the expression below. (Γ = upper case Greek letter "gamma").

Γ_T = A₁ + B₁ + B₂

We know that A₁, B₁ and B₂ are merely the shorthand notations for the symmetry species (irreducible representations). We can therefore simply write down the characters of Γ_T by adding the individual characters for A₁, B₁ and B₂ from the C_2v character table.

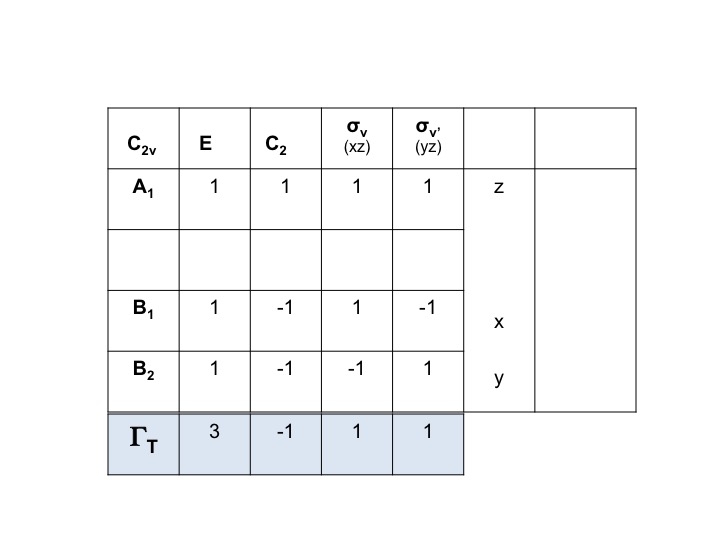
Thus Γ_T = 3  -1  1  1. 

This is a valid reducible representation and a member of the C_2v group.

In a similar manner we can write down the reducible representation for all three rotations and all the vibrations.

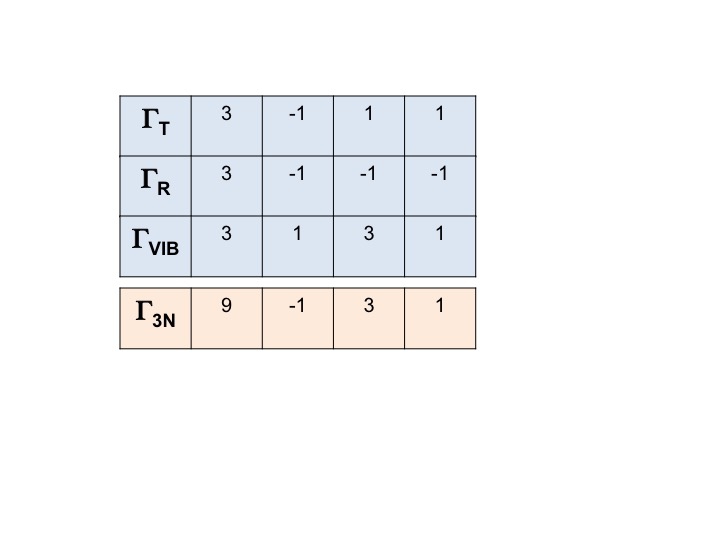
The representation for ALL the degrees of freedom for the molecule (3N) can be written as

Γ_3N = Γ_T + Γ_R + Γ_VIB

and the reducible representation for it is obtained by simply summing the characters for Γ_T, Γ_R and Γ_VIB.

Γ_3N  = 9 -1 3 1  

Make a note of this  - it will come up later!

Although the set of characters 9 -1 3 1 is a valid member of the C_2v group it is not particularly useful when discussing  molecular properties. What is really required is the language of the shorthand symmetry species (Mulliken symbols, A₁, B₁ etc.). In other words we want to express Γ_3N in terms of A₁, B₁ etc. From the information covered above it can be easily shown by inspection that:

Γ_3N = 3A₁ +A₂ + 3B₁ +2B₂

The good news is that for other more complex molecules we do not have to perform this task by inspection because:

1. We can easily generate Γ_3N as a reducible representation for a molecule (if we know its point group symmetry).

2. We can easily convert the Γ_3N reducible representation into the sum of its symmetry species (Mulliken symbols) using a "simple" formula known as the reduction formula.

General Method to Obtain Γ_3N

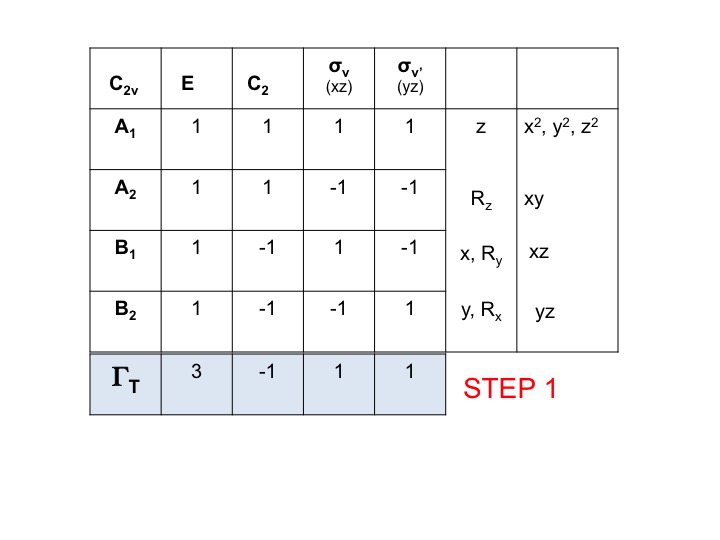
Step 1

Take the character table for the molecule and add a row at the bottom. In this row generate the reducible representation for Γ_T (or Γ_xyz) as we did above, simply by adding the characters for each operation which correspond to the molecular properties for x, y and z. For C_2v we have already shown that these are the characters corresponding to A₁, B₁ and B₂.

Step 2

Add another row below Γ_T and write down the number of atoms which DO NOT CHANGE their location during each symmetry operation. This is where you realize how useful a real molecular model set is. To do this you will also need to know where the symmetry elements are and how the symmetry operations affect the molecule. Of course, you already know how to do this because you have studied Schönflies notation and know how to assign the point group of a molecule. The character table also has all the symmetry operations listed by class along the top row.

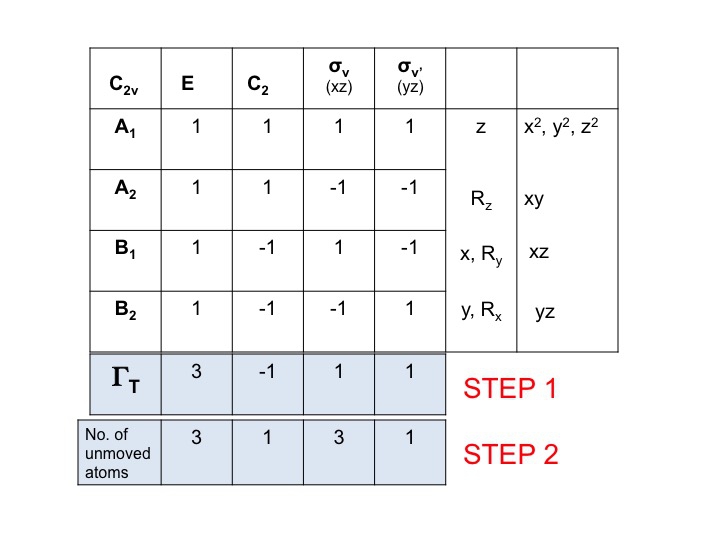
Thus for water (3 atoms) under E there are 3 unmoved atoms, but for C₂ both H's move but since the O atom sits on the C₂ axis it does not change its location and so we record 1 under the C₂ column. The new set of numbers generated in step 2 (3 1 3 1) is also a reducible representation in C_2v and obeys the rules of the group.

Step 3

In this step we simply multiply together the characters that have been generated in steps 1 and 2. The result (third row) is the reducible representation for Γ_3N (or Γ_TOT). Its that simple.

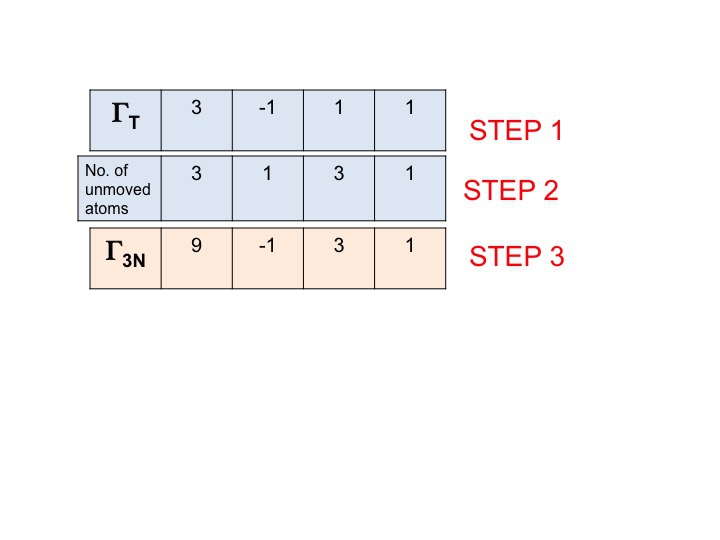
You will note that the new reducible representation (9 -1 1 3) is identical to the representation for Γ_3N that we obtained previously by inspection.

Reducing the Reducible Representation

To convert ANY reducible representation into the sum of its irreducible representations (symmetry species or Mulliken symbols) we use a reduction formula:

You can easily find this information in the character table:

Back to our example for water: Point group C_2v, order (g) = 4

The reducible representation for Γ_{3N = 9 -1 3 1}

The number of times A₁ appears in this representation is therefore

a_A1 = 1/4 { 1.1.9 + 1.1. (-1) + 1.1.3 +1.1.1} = 3

so Γ_3N contains 3 A₁ symmetry species. The numbers of the other symmetry species are calculated as follows:

a_A2 = 1/4 { 1.1.9 + 1.1.(-1) + 1.(-1).3 + 1.(-1).1 } = 1        one A₂ present

a_B1 = 1/4 { 1.1.9 + 1.(-1).(-1) + 1.1.3 + 1.(-1).1} = 3             3 B₁ present

a_B2 = 1/4 {1.1.9 + 1.(-1)(-1) + 1.(-1).3 + 1.1.1} = 2               2 B₂ present

We can now write Γ_3N = 3A₁ + A₂ + 3B₁ + 2B₂  (exactly what we got by "inspection" above. We can now subtract the symmetry species for the translations and rotations and this will give us the number and symmetry species of the fundamental modes of vibration. Γ_T and Γ_R can be obtained directly from the character table.

Γ_3N = 3A₁ + A₂ + 3B₁ + 2B₂

Γ_T = A₁ + B₁ + B₂

Γ_R = A₂ + B₁ + B₂

Γ_VIB = Γ_3N - Γ_T - Γ_R =  2A₁ +B₁

So the three normal modes of vibration for water have the symmetries A₁, A₁ and B₁.

We now have a general method for determining all of the fundamental modes of vibration for a molecule and expressing these modes in the shorthand language of Mulliken symbols. This is one of the exercises that you will be tested on in Exam 1. The best way to become confident with this method is to practice as many possible examples as you can!

Next: Selection Rules

Copyright © 2015 Richard Jones. All Rights Reserved.