The Symmetry Groups may be systematically classified by considering how to build them up using increasingly more elaborate combinations of symmetry operations. The nomenclature to denote a unique symmetry group is known as Schönflies notation. Named after the German mathematician Alfred Moritz Schönflies (1853 - 1928).
 Alfred Moritz Schönflies
Alfred Moritz Schönflies
The following outline is non-rigorous, but does give a practical scheme for use by most chemists.
Step 1: Identify very easy to classify space groups by inspection
a. Linear molecules
b. Very high symmetry molecules with multiple high order axes
a. Linear molecules: There are only two kinds of symmetry for linear molecules
i. Those with identical ends such as H2, O2, or HC≡CH. These molecules have an infinite-fold rotation axis (C∞) which coincides with the molecular axis and an infinite number of vertical symmetry planes (σv). In addition, there is a horizontal plane of symmetry (σh) and an infinite number of C2 axes perpendicular to C∞. The point group is D∞h
ii. A linear molecule with different ends has only C∞ and the σv's but no σh. Examples: CO, HCl. The point group is C∞v
b. Very high symmetry molecules
In practice molecules with very high symmetry are also relatively easy to identify by inspection. The most common of these are molecules built on a central tetrahedron, octahedron, cubooctahedron, cube, pentagonal dodecahedron or icosahedron. Of these the tetrahedron (Td) and octahedron (Oh) are the most important since they are found in many kinds of molecules.
The Tetrahedron (Td)
Examples: CH4, SiF4, ClO4-, Ni(CO)4, Ir4(CO)12
A view of some of the symmetry elements of a regular tetrahedron is shown below. The point group has a total of 24 symmetry operations. These include three S4 axes, four C3 axes, six reflection planes (σd). Note that despite the high symmetry, there is no inversion center (i) in Td.
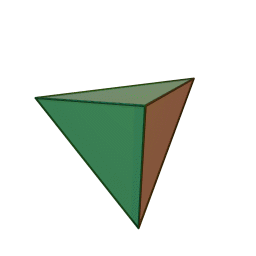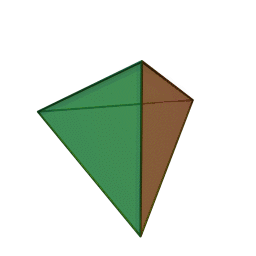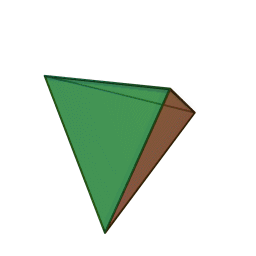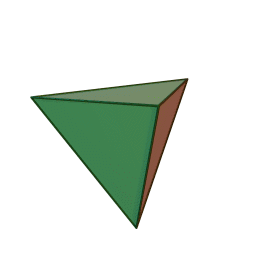
"Tetrahedron". Licensed under CC BY-SA 3.0 via Wikimedia Commons.
You can explore the various symmetry operations in more detail by going to the Otterbein University Website and clicking on any one of the Td examples.
The Octahedron and the Cube
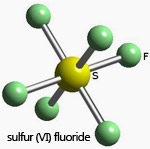
These two structures have the same symmetry elements and have a total of 48 symmetry operations. Point group symbol Oh. There are three C4 axes, four C3 axes, six C2 axes bisecting opposite edges, three σh planes, and six σd. The C4 axes are also S4 axes, and the C3 axes are S6 axes. There is an inversion center (i). Oh is an important type of symmetry since octahedral complexes such as IrCl63- and [Co(NH3)6]3+ and molecules such as SF6 are very common.
The Pentagonal Dodecahedron and the Icosahedron
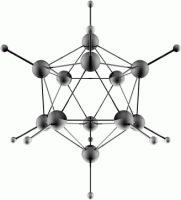
These structures are of even high symmetry and are related to each other in the same way as the octahedron and the cube - the vertices of one define the face centers of the other. They have a total of 120 symmetry operations. The icosahedral group has the symbol Ih. This is a key structural unit in boron chemistry (eg. B12H122-).
Step 2: The next step is to look for proper or improper axes of rotation
If none is found, look for a plane or center of symmetry. If a plane only is present, the point group is Cs. If a center only is present, the point group is Ci. If no symmetry element is present at all (only E), the group is the trivial one C1.
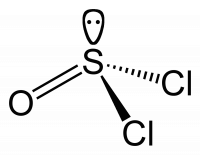
Cs: E, σ - fairly common, examples include thionyl chloride (SOCl2) and secondary amines
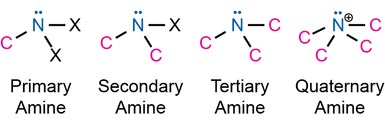
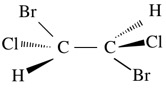
Ci: E, i - rare
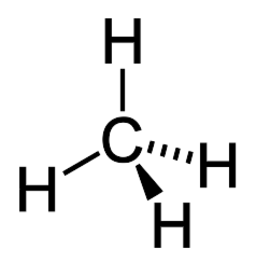
C1: E - very common, lots of organic molecules
Step 3: The Sn Groups
In rare circumstances a molecule contains an Sn axis as its only symmetry element. It can be shown that two possibilities now exist: 1) Sn where n is odd (3, 5, 7, etc.), and 2) Sn where n is even (2, 4, 6, etc.). For n odd, it can be shown that the set of operations is actually the same as Cnh. It is only for n even, that new point groups exist (S4, S6, etc.) (Note S2 = i and that point group would be Ci). Also an S4 point group has a C2 axis and an S6 point group has a C3 axis. If additional operations are possible, we are then dealing with Dnd or Dnh point groups.
Step 4: A proper or improper axis is present
If a proper or improper axis is found which is not a consequence of the presence of S2n (step 3) then we are dealing with C, or D type point groups. First, find the highest order proper axis Cn. Once identified, we look for a set of n C2 axes perpendicular to it. If this is the case then the point group is one of Dn, Dnh, or Dnd. If n C2 axes are not present, the molecule belongs to one of the C type point groups: Cn, Cnv, or Cnh.
Cn
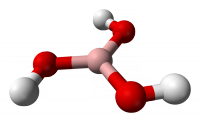
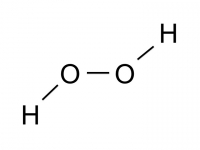
If there are no symmetry elements other than the Cn axis the point group is Cn. Molecules with this type of axial symmetry, other than C2, are rare. Examples are triphenyl phosphine (PPh3 point group C3) and non-planar hydrogen peroxide (H2O2 point group C2).


Cnv
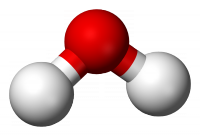
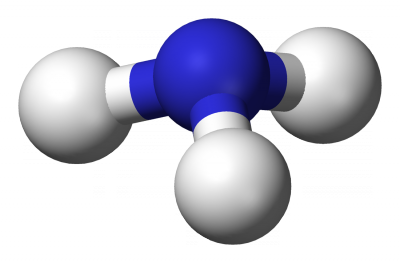
This has a proper axis (order n) plus a set of n vertical planes and is fairly common. Examples: H2O (C2v), NH3 (C3v)
Cnh
This also has a proper axis (order n) plus a horizontal plane of symmetry. These are relatively rare, examples: trans-planar H2O2 (C2h), boric acid (C3h), and trans- 1,2 - dichloroethylene.
Step 5: D Point Groups
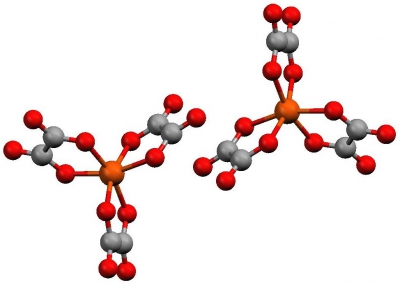
If we have a vertical Cn axis, plus a set of n C2 axes, perpendicular to it the point group is Dn. This is rare. One set of examples is the metal tris chelates such as tris (oxalato) iron (III) (D3).
Dnh
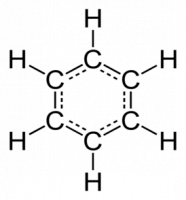
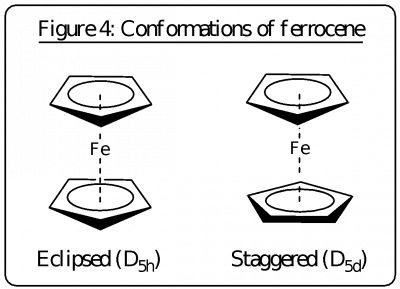
If there are additional symmetry operations possible when we get to Dn then Dnh or Dnd are possible. For example, if there is a horizontal plane of symmetry (σh) then the group is Dnh. Examples include benzene (D6h), ferrocene (Cp2Fe eclipsed) (D5h), PtCl42- (D4h), BF3 (D3h). Additional symmetry operations are reflections in vertical planes which contain the n C2 axes.
Dnd
If we add a set of vertical planes of symmetry that bisect the angles between pairs of C2 axes, we have Dnd. The easy way to distinguish this from Dnh is the absence of a horizontal plane of symmetry. Examples are staggered ethane (D3d), and staggered ferrocene (D5d).
Step 5: The Sn Groups
In rare circumstances a molecule contains an Sn axis as its only symmetry element. It can be shown that two possibilities now exist: 1) Sn where n is odd (3, 5, 7, etc.), and 2) Sn where n is even (2, 4, 6, etc.). For n odd, it can be shown that the set of operations is actually the same as Cnh. It is only for n even that new point groups exist (S4, S6, etc.) (Note S2 = i and that point group would be Ci). Also an S4 point group has a C2 axis and an S6 point group has a C3 axis. If additional operations are possible, we are then dealing with Dnd or Dnh point groups.
The 5 Steps described above can be summarized as follows:
1. Special groups? Linear (C∞v, D∞h), or high symmetry (Td, Oh)
2. No proper or improper rotation axes (C1, Cs, Ci)
3. Only Sn (n even) axis present (S4, S6, S8...)
4. Cn axis present not a consequence of S2n.
No C2's perpendicular to Cn (Cnh, Cnv, Cn)
5. Cn axis present not a consequence of S2n.
Has C2's perpendicular to Cn (Dnh, Dnd, Dn)
**At this point, it would be a good idea for you to test your knowledge by assigning point groups for various molecules. Numerous examples can be found in the homework assignments.**
Next: Character Tables
Copyright © 2015 Richard Jones. All Rights Reserved.

